짐벌락 오일러, 쿼터니언

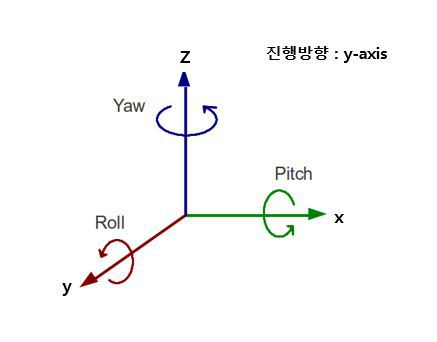
• 오일러 각: 오일러 각은 세 개의 회전 각도 (α, β, γ)로 표현됩니다. 이 각도들은 순차적으로 적용되며, 각 축에 대한 회전 행렬로 변환됩니다. 예를 들어, z축을 중심으로 α만큼 회전, y축을 중심으로 β만큼 회전, x축을 중심으로 γ만큼 회전하는 방식입니다.

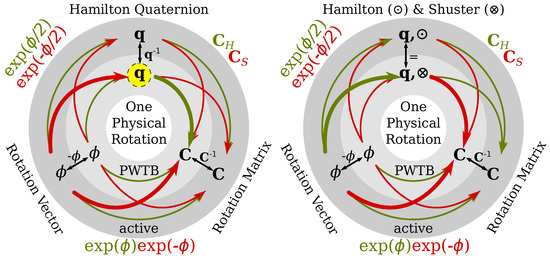
• 쿼터니언: 쿼터니언은 q = w + xi + yj + zk 형태로 표현됩니다. 여기서 w, x, y, z는 실수 성분, (xi + yj + zk는 허수부 벡터)입니다. 쿼터니언을 이용한 회전은 벡터를 쿼터니언으로 변환한 후, 회전 쿼터니언과 곱셈을 통해 수행됩니다. 회전 쿼터니언 q와 벡터 v를 회전시키는 방법은 qvq* (여기서 q*는 q의 켤레 쿼터니언)입니다.

---

3. 쿼터니언과 오일러의 장점 단점

• 오일러 각:

  • 장점: 직관적이고 이해하기 쉬우며, 각 축에 대한 회전을 명확하게 표현할 수 있습니다.

  • 단점: 짐벌락 문제(Gimbal Lock)가 발생할 수 있습니다. 이는 두 개의 회전 축이 일치하게 되어 자유도가 감소하는 현상입니다. 또한, 회전의 순서에 따라 결과가 달라지므로, 일관된 회전 표현이 어렵습니다. 짐벌락이 발생하는 근본적인 이유는, 오일러의 회전축이 서로 hierachy로 구성되어 있기 때문입니다.

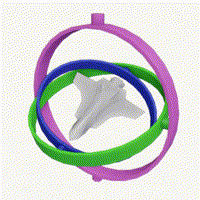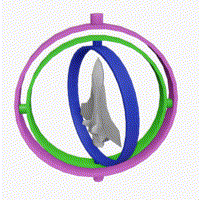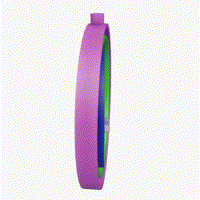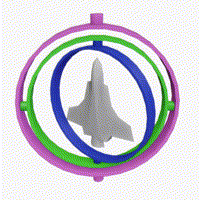
• 쿼터니언:
  • 장점: 짐벌락 문제를 피할 수 있으며, 회전의 누적 계산에서 수치적 안정성을 제공합니다. 또한, 쿼터니언은 회전의 보간(Slerp)에서 부드러운 전환을 가능하게 합니다.

• 단점: 직관적으로 이해하기 어렵고, 4개의 성분을 다루어야 하므로 계산이 복잡할 수 있습니다. 또한, 쿼터니언의 180도 회전 제한 문제도 존재합니다. 그 이유는 쿼터니언 곱을 수행할 때, 서로 반대 방향으로 축은 상쇄되지만 회전 각도는 두 배로 증가하기 때문이다 (복소평면을 기준으로 보자면)